Redes Neurais 2: Perceptrons de Rosenblatt

“For me there is no absolute knowledge: everything goes only by probability. Both Descartes and Schelling explicitly reported an experience of sudden illumination when they began to see everything in a different light.”
Wang, H. (1996)

Eu acho fundamental (e interessante à beça) alinhar a história com o pensamento, vamos começar então pelo começo.

História e filosofia por trás do perceptron de Rosenblatt

Com o advento do computador, as idéias de McCulloch e Pitts puderam ganhar um pouco mais de tangibilidade. Já éramos capazes de construir máquinas para realizar cálculos por nós.

Frank Rosenblatt, psicólogo estadunidense, sugeriu um método de aprendizado computacional. Seu objetivo era transcrever o “mundo dos fenômenos”, mundo que nós, humanos, estamos familiarizados, para uma “linguagem”, de modo que um computador pudesse receber estes “fenômenos” como entradas. Como ele mesmo explica:

Since the advent of electronic computers and modern servo systems, an increasing amount of attention has been focused on the feasibility of constructing a device processing such human-like functions as perceptions, recognition, concept formation, and the ability to generalize from experience. In particular, interest has centered on the idea of a machine which would be capable of conceptualizing inputs impinging directly from the physical environment of light, sound, temperature, etc. — the “phenomenal world” with which we are all familiar — rather than requiring the intervention of a human agent to digest the code has necessary information.

Frank Rosenblatt (1957) [1]

O objetivo do perceptron, segundo Rosenblatt, é ilustrar de maneira geral algumas das propriedades fundamentais de um sistema inteligente sem se apegar as condições, muitas vezes desconhecidas, de um sistema biológico [2, p2-3].

Os componentes de um perceptron são:

Uma arquitetura de rede;
Neurônios MCP;
Uma Regra de Aprendizado.

Na época causou uma grande euforia, porém sem as necessárias ferramentas teóricas e sem a devida capacidade computacional (como o algoritmo de back propagation de 1986), o machine learning ficou durante um bom tempo sem ter alguma aplicação prática. Hoje em dia, têm aplicações em quase os todos campos da ciência e impacto direto na nossa vida.

Matemática

Atualmente, o perceptron é um conceito que já foi generalizado em termos de machine learning. O perceptron pertence a categoria de aprendizado supervisionado (vou escrever sobre isso mais pra frente). De maneira simplificada isto quer dizer que o modelo, em sua fase inicial, não sabe nada (que seja útil pelo menos, pois começa com um estado aleatório) e se corrige (diminui seu erro) para aprender o que estamos ensinando a ele.

O perceptron resolve uma categoria específica de problemas, os chamados problemas de classificação binária. Como vamos ver, o perceptron consegue aprender a classificar pontos em um plano e atualizar sua estimativa conforme novas observações são adicionadas.

Função de ativação

A função de ativação (leia-se o que faz o neurônio artificial se ativar ou desativar), ou seja, o output y, é definido como sendo:

\[
y=g\left(\sum ^{M}_{j=0} I_{j} \ .\ w_{j}\right) =g\left( w^{T} I\right)
\]

Onde I são os inputs do perceptron, w os pesos relacionados a cada input e g uma “função degrau”. Essa função degrau determina basicamente qual classe o perceptron “ativou”. Vamos convencionar para simplificar a utilização das classes “-1” e “1”. Portanto nossa função degrau g pode ser definida como sendo:

\[
g(z)=\begin{cases} 1 & \text{if } z\geq \theta \ -1 & \text{caso contrário} . \end{cases}
\]

Onde θ é o nosso limite, valor limite, ou threshold, como é comum na literatura em inglês.

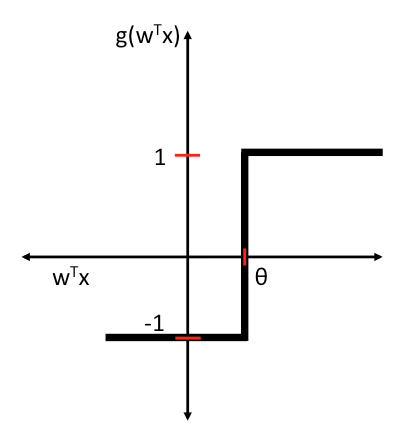
Função degrau utilizada como função de ativação [3].

Essa abordagem está de acordo com a regra “all-or-none” que escrevi no post anterior.

De maneira simplificada: o output do perceptron é calculado por uma função degrau que leva como parametro a soma dos inputs vezes os pesos de cada input. Se a soma for > que um número qualquer (inicialmente aleatório), o output é “1”. Caso contrário “-1”.

É fácil notar que pesos (w) e o valor de threshold (θ) são as variáveis que podemos corrigir aqui, certo? É é justamente onde acontece a aprendizagem.

Aprendizagem

A ideia de Rosenblatt começa a ficar interessante nesse momento. A diferença é que o algoritmo proposto por ele é capaz de aprender (se ajustar com o intuito de diminuir o erro) os pesos para os sinais de input. Assim, após um determinado número de interações, o perceptron espontaneamente aprende o que estamos ensinando a ele, nesse caso separar os inputs em duas categorias -1 e 1.

Para aprender, o perceptron segue o seguinte algoritmo:

Defina os pesos w dos inputs I como números aleatórios;
Para cada conjunto de percepções (ou observações):
1. Calcule o output do perceptron utilizando a função de ativação g;
2. Atualize os pesos do perceptron para que se aproxime da resposta correta.

O calculo de atualização dos pesos é a etapa mais bela desse algoritmo. Para cada iteração, vamos atualizar os pesos levando em consideração o peso anterior e o quão errado ele estava, usando, para isto, o valor “alvo” (esperado) e o valor “saida” (encontrado):

\[
w_{j} =w_{j} +\Delta w_{j}\\
\]

Onde:

\[
\Delta w_{j} =\eta \ (\text{alvo}^{(i)} -\text{saida}^{(i)} )\ x^{(i)}_{j}
\]

e η é a taxa de aprendizado (learning rate), geralmente um número bastante pequeno, utilizado para que o perceptron não fique procurando a solução ideal muito longe, “alvo” é a label real do objeto e “saída” a label que o perceptron julgou ser verdadeira.

É interessante notar que caso o perceptron julgue uma label como correta, o delta será zero:

\[
\begin{array}{l}
\Delta w_{j} =\eta (-1^{(i)} – -1^{(i)} )\ x^{(i)}_{j} =0\\
\Delta w_{j} =\eta (1^{(i)} -1^{(i)} )\ x^{(i)}_{j} =0
\end{array}
\]

Desta maneira, a cada nova interação, os pesos são corrigidos e atualizados de modo que esteja cada vez mais próximo do resultado verdadeiro das observações que entregamos a ele.

Um abraço!