Com os conceitos dos posts anteriores e todo esse embasamento, vamos seguir aos notebooks Jupyter!
Eu gosto de começar um projeto pensando em como podemos representá-lo em classes. Parece razoável pensar em uma classe Perceptron com alguns métodos que falamos anteriormente.
Minha estratégia de implementação será:
- Discutir minha definição de classe do Perceptron;
- Implementar os métodos concretos;
- Determinar um data set de exemplo para um teste;
- Ver se o perceptron aprende mesmo.
Definindo a classe Perceptron
Vamos pensar em quais atributos e métodos vamos precisar para desenhar nossa classe Perceptron.
Atributos
- Taxa de aprendizagem (η);
- Número de Epochs (para mais informações, veja [1]);
Métodos
- Método para a função ativação:
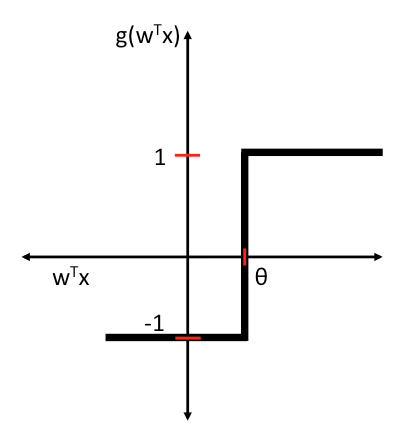
_activation(X);- Descrição: Como função de ativação, escolhi a função degrau, descrita no post anterior. Outras funções são comuns para esta finalidade (para mais informações, veja [2]).
- Método para a função soma:
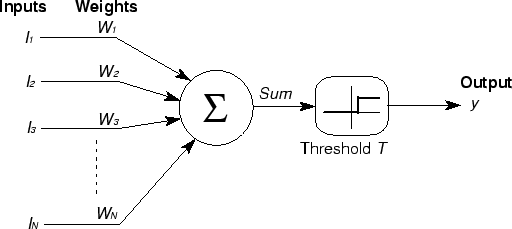
_sum(X);- Descrição: O processo de sum vai multiplicar X pelo peso correspondente.
- Método para iniciar um treinamento:
fit(X, y);- Descrição: É o método que vai de fato colocar as epochs para rodar, calcular os erros e manter um historico de erros na lista
_errors.
- Descrição: É o método que vai de fato colocar as epochs para rodar, calcular os erros e manter um historico de erros na lista
- Método para gerar uma predição:
predict(X);- Descrição: Passa o input X para a função de soma e de ativação e retorna a classe esperada.
Implementação
import numpy as np
class Perceptron(object):
"""
Um perceptron simples com componentes simples.
"""
def __init__(self, learning_rate=0.01, epochs=50, verbose=False):
"""
Inicializa o perceptron com os valores de
learning rate (taxa de aprendizado), epochs e um
parametro de verbose, sinalizando que queremos ver os detalhes
do funcionamento.
"""
self.verbose = verbose
self.learning_rate = learning_rate
self.epochs = epochs
if(self.verbose):
print("[>] Perceptron parameters:\n- learning rate: {}\n- # epochs: {}".format(
self.learning_rate,
self.epochs
))
def _sum(self, X):
"""
O processo de sum vai multiplicar o input pelo peso.
"""
dp = np.dot(X, self._weights) + self._bias
if(self.verbose):
print("[!] Aggregation ({} and {}) + weight {} = {}".format(
X,
self._weights,
self._bias,
dp
))
return dp
def _activation(self, value):
"""
Como função de ativação, escolhi a função degrau.
Outras funções são bem comuns, mas o ganho entre elas
faz com que a degrau seja uma das com melhor custo-benefício.
"""
return np.where(value >= 0.0, 1, -1)
def fit(self, X, y):
"""
Vamos começar com os pesos como um array
numpy aleatório, já que não temos pistas sobre
quais são os pesos corretos.
"""
self._bias = np.random.uniform(-1, 1)
self._weights = np.random.uniform(-1, 1, (X.shape[1]))
self._errors = []
if(self.verbose):
print("[>>] Starting training routine:\n- initial weights: {}\n- initial errors: {}".format(
self._weights,
self._errors
))
print("- train set (X): {}\n- train set (y): {}\n---".format(
X,
y
))
# Iterando o numero de epochs...
for epoch_number in range(self.epochs):
errors = 0
if(self.verbose):
print("[>>] Entering epoch {}\n- weights: {}\n- errors: {}".format(
epoch_number,
self._weights,
self._errors
))
for xi, target in zip(X, y):
if(self.verbose):
print("[!] Learning xi = {} (target {})".format(xi, target))
output = self.predict(xi)
update = self.learning_rate * (target - output)
if(self.verbose):
print("[!] {} = {}({} - {})".format(
update,
self.learning_rate,
target,
output
))
print("[<] weights was {}".format(self._weights))
self._bias += update
self._weights += update * xi
if(self.verbose):
print("[>] weights are now {}".format(self._weights))
errors += int(update != 0.0)
if(self.verbose):
print("-")
self._errors.append(errors)
if(self.verbose):
print("--")
return self
def predict(self, X):
result = self._activation(self._sum(X))
if(self.verbose):
print("[?] Should fire? (is >= 0): {}".format(
result
))
return resultTeste
Vamos testar nosso perceptron! Para fazer isso, vamos utilizar um método muito pratico do sklearn, o make_blobs. Este método cria dados concentrados em volta de um ponto. É bastante util para gerar dados para testes de regressão e classificação. Nosso perceptron é capaz de aprender a classificar dados lineares.
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
# Vamos criar 2 blobs com 200 samples e 2 features (2 dimensões) e 2 centros.
blobs = make_blobs(n_samples=200, n_features=2, centers=2)
# Em seguida, vamos plotar os dados gerados para visualização.
plt.scatter(blobs[0][:,0], blobs[0][:,1], c=blobs[1])
plt.show()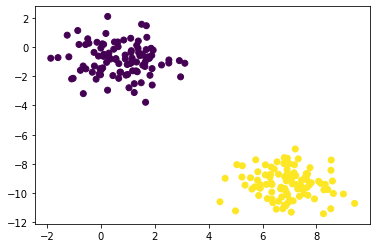
Pronto. Vamos colocar nosso perceptron para rodar e classificar os blobs.
Para isso, basta inicializarmos a nossa classe anterior, separar os X (features) e o y (classe).
Vamos em seguidar rodar o comando fit do perceptron para treinar os pesos.
ppn = Perceptron(epochs=50, learning_rate=0.01, verbose=False)
X = blobs[0]
y = blobs[1]
# Apenas para substituir as classes 0 e 1 para 1 e -1
# A classe 1 é a que desejamos encontrar.
y[y == 0] = -1
ppn.fit(X, y)Após alguns segundos de treinamento, nosso perceptron já vai ter aprendido os pesos para classificar os blobs.
Com a ajuda do método plot_decision_regions da lib mlxtend, podemos plotar a região de classificação:
from mlxtend.plotting import plot_decision_regions
plot_decision_regions(X, y, clf=ppn)
plt.title('Perceptron')
plt.show()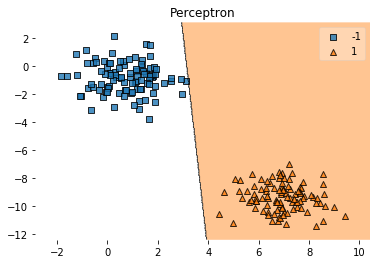
Vamos também dar uma olhada no histórico de erros:
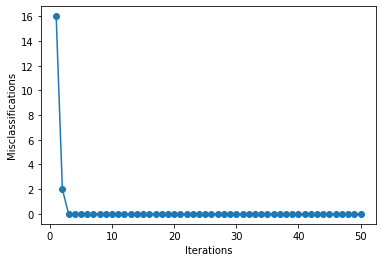
Conforme os pesos foram sendo corrigidos, o perceptron passa a classificar 100% dos pontos de maneira correta.
Espero que tenha sido interessante para você leitor como foi pra mim construir essa série de posts sobre Machine Learning!
Até a próxima!
Bibliografia
[1] https://towardsdatascience.com/epoch-vs-iterations-vs-batch-size-4dfb9c7ce9c9